토질역학 압밀 시험 목적
압밀실험을 통하여 압밀 정수(압축지수, 선행압밀하중, 체적압축계수, 압밀계수)를 구할 수 있으며, 압밀정수를 이용하여 점성토 지반이 하중을 받아서 지반 전체가 1차원적으로 압밀 되는 경우에 발생되는 침하특성(침하량, 침하 속도)을 밝히는 데 있다.
토질역학 압밀 시험 장비
압밀용기
압밀용기는 다음의 것으로 구성되며 압력에 의해 변형되지 않는 충분한 강성을 가진 것.

- 압밀링 : 압밀링은 내면이 매끄러운 링으로 안지름 6cm, 높이 2cm를 표준으로 한다. 스테인리스강 등의 녹슬지 않는 재질로, 흙과의 마찰이 적은 것을 사용한다. 또한 최대 압밀 압력시의 안 지름 변화는 0.05% 이하인 것.
- 가이드링 : 압밀링과 같은 안지름으로 높이가 가압판의 바깥둘레의 높이와 같은 정도의 것
- 가압판 : 중심에 재하점이 있는 강철 원판으로 다공판을 가지며 가이드링 및 압밀링 안을 매끄럽게 움직이는 것.
- 밑판 : 압밀링을 고정하는 강철판으로 다공판을 가진 것.
- 다공판 : 충분한 강성을 가지며 투수계수가 10-4cm/s이상이며 흙 입자가 들어가지 않을 정도로 틈이 적은 것.
- 수침용기 : 압밀용기 내의 시험체를 수침상태로 유지할 수 있는 것.
- 재하장치 : 재하장치는 압밀용기를 수평으로 지지하고 소정의 하중을 시험체에 충격 및 편심 없이 단시간에 가할 수 있는 것.
- 변위계 : 예상되는 시험체의 총압밀량이 10mm 미만인 경우는 0.002mm까지, 10mm 이상인 경우는 0.01mm까지 측정할 수 있는 것을 표준으로 한다. 다이얼게이지 또는 이것과 동등 이상의 성능을 가진 전기식 변위계를 사용한다.
시험체의 제작 기구

- 트리머 : 시료를 압밀링 안지름보다 약간 큰 원반 모양으로 성형할 수 있으며, 성형한 시료에 커터링을 수직으로 압입 할 수 있는 것.
- 커터링 : 압밀링과 같은 안지름을 가진 내면이 매끄러운 링으로 그 한 끝은 예리한 칼로 되어 있고 다른 한 끝에는 압밀링을 부착할 수 있는 것.
- 시험체 압입 원판 : 지름은 압밀링보다 0.3mm 정도 작은 것.
- 줄 톱 : 줄의 지름이 0.2mm 정도인 것.
- 곧은 칼 : 곧은 칼은 강제이며 한쪽 날이 붙은 것.
- 칼
기타 기구
- 저울,
- 버니어 캘리퍼스,
- 함수비 측정 기구,
- 시계,
- 실리콘 오일 또는 실리콘 그리스
토질역학 압밀 시험 방법
1. 공시체 제작 및 시험기 조정
- 압밀링의 무게와 높이 및 안지름을 버니어 캘리퍼스로 측정한다.
- 흙 샘플에서 시료를 끄집어내어 압밀링의 안 지름 및 높이보다 10mm 정도 크게 깎는다. 이것을 트리머에 올려놓고, 지름이 링의 안 지름 보다. 2-3mm 정도 크게 깎는다. 깎아낸 시료는 함수비와 흙 입자의 비중을 측정하기 위하여 보존한다.
- 압밀링 위에 성형한 공시체를 올려놓고 줄 톱이나 곧은 날로 그 주변을 깎으면서 링 속으로 조심 해서 밀어 넣는다. 이때 링과 시료사이에 공간이 생기지 않도록 주의한다.
- 시료를 링 속으로 완전히 밀어 넣은 다음 압밀링 위아래 면에 나와 있는 부분의 시료를 링 끝 면 을 따라 잘라낸다.
- 성형이 완료된 공시체는 링과 함께 무게를 측정한다.
2. 시험준비
- 포화된 시료일 때에는 링 내부에 될 수 있는 대로 공기가 남아 있지 않도록 압밀용기를 조립하고, 필요하다면 수중에서 조립한다. 이때 가압판과 밑판의 다공판을 미리 물속에 담아 두었다가 사용해야 한다. 불포화시료 일 때에는 압밀용기의 조립은 공기 중에서 행한다.
- 물에 적신 여과지를 공시체에 위아래 면에 붙이고 이것을 밑판의 다공석반 위에 올려 놓는다.
- 가압판을 공시체 위에 올려놓는다.
- 포화된 시료일 때에는 수침상자의 수위를 가압판의 다공석반이 침수될 정도로 한다. 불포화 시료로서 흡수성이 있을 때에는 수침상자에 물을 넣지는 않으나 수분의 증발을 방지하는 처리를 하여야 한다.
3. 하중 재하 및 Rebounding
- 조립한 압밀용기를 재하장치에 올려놓는다.
- 다이얼 홀더를 상하로 조정하여 침하량 측정용 다이얼 바늘을 장치하고 영으로 맞춘다. 압밀이 진 행하면 바늘이 빠져나온다는 것을 주의한다.
- 0.05kg/cm²의 하중을 얹고 24시간 동안 공시체를 정말포화시킨다.
- 24시간이 지난 후 공시체에 0.1kg/cm²의 압력이 가해지도록 하중을 얹고 경과 시간에 대한 침하 량을 기록한다. 경과 시간은 0, 0.1(8초) ,0.25(15초), 0.5(30초), 1분, 2분, 4분, 8분, 15분, 30분, 60분, 120분, 240분, 480분, 1440분으로 측정한다.
- 24시간(1440분)이 지나면 그다음 단계의 하중 즉 0.2kg/cm² 압력이 되도록 하중을 가한 다음 ④ 번에서와 똑같은 방법으로 경과 시간에 대한 침하량을 기록한다.
- 이와 같은 방법으로 다음의 하중을 순서대로 가하면서 7일 동안 경과시간에 대한 침하량을 기록한 다. (0.10, 0.20, 0.40, 0.80, 1.60, 3.2, 6.4kg/cm² - 7단계)
- 압밀 시험은 시험 중 시료가 건조되기 쉽다. 따라서 시험 중에 접시에 물이 흘러내리기 직전까지 물을 자주 채워 건조를 방지해야 한다.
- 시험이 완료되면 압밀 시험기를 해체한 다음 물을 깨끗이 닦아내고 무게를 잰다. 다음에는 시료를 꺼내어 건조로 속에서 말린다.
- 건조로 속에서 건조한 시료의 무게를 측정한다.
토질역학 압밀 시험 이론
1. 흙의 압축
토질역학적인 관점에서 흙의 압축성에 의한 결과인 침하에는 즉시침하와 압밀침하가 있다.
① 즉시침하(immediate sttlement) 하중을 받은 후 단시간 내에 압축되는 현상이다. 공학적으로 보면 흙 입자와 물은 비압축성이므로 흙의 압축성은 흙 입자 사이의 간극이 감소되어 일어나는데, 이때 간극 속에 있는 물이나 공기가 빠 져나가게 된다. 일반적으로 즉시침하는 사질토에 크게 일어나며, 점성토의 경우 즉시침하량은 아주 작다.
p = q [B(1-mu^2)] / E * I
( q: 등분포하중, B: 재하면적의 폭, mu: 푸아송비, E: 변형계수, I: 영향계수 )
② 압밀침하(consolidation settlement)
- 1차 압밀 : 포화된 흙이 하중을 받아 과잉간극수압이 발생하고 이 간극수압이 배수로 인해 체적이 감소되면서 응력이 수압으로부터 토립자내응력 즉 유효응력으로 이전되고 이 증가된 유 효응력으로 인해서 체적변화 즉 압축이 일어나는 과정을 “압밀(壓密)”이라 하며, 특히 1 차압밀(Primary consolidation)이라 한다. 일반적으로 포화된 점토는 즉시침하량보다 압 밀침하량이 훨씬 크며, 또 침하에 소요되는 시간도 길어져서 주로 문제가 되는 것은 압 밀침 하이다.
- 2차 압밀 : 1차 압밀이 완료된 후 즉 과잉간극수압이 완전히 소산된 후에도 계속해서 일어나는 압축 을 2차압축(Secondary compression) 또는 2차압밀(Secondary consolidation)라고 한 다. 즉 2차압축을 유효응력이 일정한 상태, 즉 과잉간극수압의 변화가 0인 상태에서 발생한다. 2차압축은 1차압밀 중에 일어나는 구조적 교란이 점차적으로 안정된 구조로 재조정되는 과정으로서 2차 압축량은 점토광물표면의 점성이 대단히 큰 흡착수막에 의해 서 결정된다. 유기질 점토의 경우 2차 압축량이 크다.
2. 압밀의 문제
공학적인 관점에서 압밀의 문제는 다음의 두 가지 문제로 귀착된다.
- 압밀침하량이 얼마냐 하는 문제이다. 모래지반과 달리 점토지반의 침하량은 일반적으로 무척 크기 때문에 항상 문제점을 내포하게 되며, 따라서 전체 압밀침하량을 예측하는 것이 중요한 문제이다.
- 압밀침하량이 얼마나 긴 시간에 걸쳐 일어나느냐 하는 점이다. 점토지반에 있는 물이 모래, 지반 등의 배수층으로 빠져나가야만 침하가 일어나므로 일반적으로 침하는 아주 천천히 일어나게 된다. 따라서 침하가 일어나는 속도를 알아야 한다. 물이 빠져나가는 원리는 투수문제로서 투수방정식을 풀음으로써 이를 예측할 수 있다.
- 예측한 최종압밀침하량과 압밀침하속도(50% 또는 90%까지 압밀이 일어나는데 소요되는 시간)를 가지고 연약지반 위에 제방을 쌓거나 고속도로 등의 구조물을 건설하여야 할 때 성토고와 공사기간의 결정 외에 허용침하량에 의한 설계를 하는 경우에 사용된다.
3. Terzaghi의 기본 압밀 이론
① Terzaghi 압밀이론식의 기본가정 - 점토층은 균질(homogeneous)하다.
- 점토층은 완전히 포화되어 있다. ( = 100%)
- 물 입자와 흙 입자는 비압축성이다.
- 물의 흐름방향과 압축방향은 1차원(연직방향)이다.
- Darcy의 법칙이 성립한다. ()
② 압밀의 기본 미분방정식

③ 압밀계수

4. 압축계수(coefficient of compressibility)
압밀시험에서 점토시료에 작은 하중에서 큰 하중을 계단상으로 가하면 그때 그때의 응력(σ)에 대 한 간극비(e)를 구할 수가 있는데 이를 plot 하고 ∂-e곡선의 기울기를 압축계수라 하며 이는 침하 량을 구하기 위한 계수이다. 시료를 압축하는 경우에 비해서 압력(∂)을 제거하면서 ∂-e곡선을 plot 하면 그 구배가 훨씬 완만하게 된다. 시료에 가해졌던 초기압력 ∂1이 △∂만큼 증가되어 ∂2로 되면 간극비도 e1에서 e2로 △e만큼 감소하게 되며 ∂'-e곡선의 구배는

이 되며 av를 압축계수라 한다.
5. 체적압축계수(coefficient of volume compressibility)
유효응력의 증가에 대한 체적변화율(간극비 변화율)로 정의되며, mv의 단위는 압력의 역수이다. 이것을 식으로 표시하면
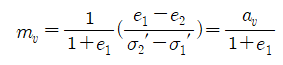
어떤 흙에 대한 mv의 값은 일정한 값이 아니며, 그 값은 계산하고자 하는 압력의 범위에 따라 달라진다.
6. 압축 및 체적압축계수와 침하량의 관계
앞서 말한 Terzaghi의 이론에 따르면 압밀은 1 축적이기 때문에 체적변화는 시료높이의 변화로 표시할 수 있다.

여기서, H : 시료의 높이(cm) △H: 시료높이의 변화(침하량)(cm)
따라서 침하량을 구해 보면

7. 압축지수(compression index)
e- log∂' 압밀곡선에서 선형을 띠는 직선 부분(처녀압축곡선-virgin compression line)의 기울기를 압축지수(compression index)라고 한다. 압축지수 Cc는 다음 식으로 표시된다.

압축지수의 값은 흙이 연약할수록 크고 견고할수록 작으며, 압밀침하량을 계산하는 데 쓰이는 중요 한 값이다. 이 식에서 부의 기호는 압력의 증가에 대하여 간극비는 감소한다는 것을 뜻하므로 Cc는 결국 양의 값을 가진다.
8. 선행압밀응력
① 선행압밀하중 세로축에 간극비, 가로축(대수눈금)에 응력을 잡아 반대수용지에 그래프를 그리면 곡선의 처음 부분은 그 기울기가 완만하나, 어느 하중 이상이 되면 갑자기 급해져서 거의 직선상을 보이는데 그 경계가 되는 하중을 선행압밀응력(preconsolidation pressure)이라고 하며 그 크기는 그 흙의 응력경력(stress history)에 의존한다. 실제로는 이 곡선의 경사가 완만하게 증가하기 때 문에 그 경계를 명확히 구분하기 힘들다.
② Casagrande는 선행압밀하중을 결정하는 방법을 다음과 같이 제시하고 있다. 먼저 간극비-하중곡 선(압밀곡선이라고도 함)에서 곡률이 가장 큰 점을 선택하며 그 점을 통하는 수평선과 접선을 긋는 다. 이 두 선분으로 이루어지는 각도를 2 등분한 선이 이 곡선의 직선 부분의 연장선과 만나는 점에 대응하는 하중이 선행압밀하중이 된다.
③ 정규압밀점토(Normally consolidated clay, NC clay) 현재 받고 있는 상재압력이상의 응력을 받은 적이 없는 점토를 말하며 따라서 현재의 상재압력이 이 점토가 받은 최대응력이다.
④ 과압밀점토(Overconsolidated clay, OC clay) 현재 받고 있는 상재압력보다 더 큰 응력을 받았던 응력이력을 갖고 있는 점토를 말하며, 같은 조 건 하에서 과압밀 점토는 정규압밀점토보다 단단함이 일반적이다.
⑤ 과압밀비(Overconsolidation Ratio, OCR)
OCR = ∂' m / ∂0'
∂' m= 선행압밀응력, ∂0' = 현재의 유효상재압력
9. 압밀계수
- 압밀계수(coefficient of consoldation)는 지반의 압밀침하시간을 추정하는데 쓰이는 중요한 값이다. 그 단위는 [L^2T^-1]로서 ㎠/sec, ㎡/day 등이다. Cv값이 큰 점토일수록 압밀진행속도가 빠름을 나타 낸다.

에서 같은 점토에서도 압밀이 진행될수록 투수계수와 체적변형계 수가 변함으로 Cv값도 시간에 따라 변할 것이다. 다만 시간이 감에 따라 K와 Mv 가 동시에 감소하므로 Cv값은 거의 일정하다고 가정한다.
- 압밀계수의 값은 압밀시험을 할 때 시료의 시간-침하량곡선으로부터 구해지며, 이것을 구하는 방법 에는 루트 T방법과 log T방법의 두 가지가 있다.
① log T방법 : 세로축에 침하량을 적고 가로축에 시간(대수눈금)을 적어 측정값을 점찍으면 곡선을 얻을 수 있다.
- 두 개 곡선의 접선이 만나는 점이 과잉간극수압의 완전소산을 의미하는 100% 일차 압밀 완료점을 의미한다.
- 반대수지 상에서는 시간 T=0 인 초기점을 찍을 수 없으므로 곡선의 처음 부분은 포물선이 된다 고 가정하고, T=0에서의 다이얼 읽음을 다음과 같이 결정한다. t=t1인 점(B)과 t2=4t 1되는 점(C)을 표시한다. B점과 C점 사이의 변형량을 x라고 할 때 B점으로부터 위쪽으로 x만큼 표시하 고 이때의 값을 d0, 즉 t=0일 때의 초기값으로 가정한다.
- d0점과 d100점의 중앙점이 d50점으로서 50%의 압밀을 나타내는 점이다. 이때의 시간 t50이 50% 압밀에 소요되는 시간이다.
- 압밀계수는 다음 식으로부터 구할 수 있다. t50=0.197이므로

- Hdr은 압밀시료의 배수거리로서 단면배수일 때에는 시료의 전두께를 취하고, 양면배수일 때에는 전두께의 반을 취한다.

② √T방법 : 어떤 임의의 한 하중에 대한 시간
-침하량곡선을 그리는 데 있어서 세로축에는 침하량을, 가로축에는 √T표시하여 측정결과를 plot 하여 그래프를 그린다.
- 침하량 - √T곡선의 처음 부분으로부터 접선을 긋는다. 이때 접선이 종축과 만나는 점이 A이다.
- 위의 접선 기울기의 1.15배가 되는 선분을 긋고 곡선과 만나는 점이 √T90이 되는 점이다.
- 90%에 압밀에 소요되는 시간계수 T90=0848 이므로 다음 식으로 압밀계수를 구한다.


10. 1차 압밀비
시료가 외부하중을 받아 발생하는 압축량은 과잉 간극수압이 소산 되어 발생되는 압밀량과 과잉간극 수압이 완전히 소산 된 후 발생되는 2차 압축량의 두 가지로 나누어진다. 전자는 Terzaghi의 압밀 이 론에 따른 1차 압밀(Primary Consolidation)이라 하고, 후자는 2차 압축(Secondary Consolidation)이 라고 하며, 이것은 압밀이론을 따르지 않는다. 전체 압축량 중에 1차 압밀로 인한 압축량의 비율을 1차 압밀비 rp라고 하며, 시간 -침하량 곡선을 이용하여 √T방법 또는 log T방법에 따라 다음의 공식을 이용하여 구한다.


11. 2차 압밀
과잉간극수압이 100% 소산 되면 일차압밀은 완료되었다고 본다. 그러나 그 이후에도 계속하여 발생하는 침하를 2차 압밀이라고 한다.
- 2차 압축지수(secondary compression index)

- 2차 압밀침하량 :

ep : 1차 압밀 완료 시의 간극비, H : 점토층의 두께
토질역학 압밀 시험 결과
1. 하중 0.1 ㎏/㎠일 때 √T와 log T그래프


2. 하중 0.2 ㎏/㎠일 때 √T와 log T그래프

3. 하중 0.4 ㎏/㎠일 때 √T와 log T그래프

4. 하중 0.8 ㎏/㎠일 때 √T와 log T그래프

5. 하중 1.6 ㎏/㎠일 때 √T와 log T그래프

6. 하중 3.2 ㎏/㎠일 때 √T와 log T그래프

7. 하중 6.4 ㎏/㎠일 때 √T와 log T그래프

8. 선행압밀응력 그래프

9. 하중과 시간에 따른 압밀 그래프

| 날짜 | 무게 (0.1kg/㎠) | 시간 (초) | 무게 (0.2㎏/㎠) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 15 | 30 | 60 | 2m | 4m | 8m | 15m | ||
| 10월 26일 | 0.1 | 0.39 | 0.39 | 0.39 | 0.39 | 0.39 | 0.39 | 0.4 | |
| 10월 27일 | 0.2 | 0.43 | 0.46 | 0.46 | 0.47 | 0.47 | 0.48 | 0.46 | |
| 10월 28일 | 0.4 | 0.53 | 0.57 | 0.58 | 0.59 | 0.61 | 0.63 | 0.66 | |
| 10월 29일 | 0.8 | 0.7 | 0.81 | 0.82 | 0.85 | 0.87 | 0.9 | 0.92 | |
| 10월 30일 | 1.6 | 0.97 | 1.07 | 1.12 | 1.17 | 1.21 | 1.25 | 1.26 | |
| 10월 31일 | 3.2 | 1.36 | 1.49 | 1.53 | 1.58 | 1.61 | 1.66 | 1.68 | |
| 1월 1일 | 6.4 | 1.72 | 1.86 | 1.91 | 1.94 | 1.96 | 1.99 | 2.02 | |
| 무게 (kg) | 갭 비율 (e) | 평균 면적 (cm²/kg) | 체적 압축 계수 (mv) (cm²/kg) | Hdr (cm) | t90 (분) | 하중에 의한 응축 계수 (cv) | 루트 t50 (분) | 하중에 의한 응축 계수 (cv) (로그 t) | 침투도 계수 k (cm/min) |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.9185777 | - | - | - | - | - | - | - | - |
| 0.1 | 0.9185394 | 0.0004 | 0.0002 | 1.0000 | - | - | - | - | - |
| 0.2 | 0.9184434 | 0.0010 | 0.0005 | 1.0000 | - | - | - | - | - |
| 0.4 | 0.9182803 | 0.0008 | 0.0004 | 0.9999 | - | - | - | - | - |
| 0.8 | 0.9180213 | 0.0006 | 0.0003 | 0.9998 | - | - | - | - | - |
| 1.6 | 0.9176472 | 0.0005 | 0.0002 | 0.9996 | 11.56 | 7.33E-02 | 1.10 | 1.79E-01 | 3.08E-08 |
| 3.2 | 0.9173019 | 0.0002 | 0.0001 | 0.9994 | 4.00 | 2.12E-01 | 0.80 | 2.46E-01 | 2.58E-08 |
| 6.4 | 0.9169469 | 0.0001 | 0.0001 | 0.9992 | 3.24 | 2.61E-01 | 0.65 | 3.03E-01 | 1.63E-08 |
| 번호 | 1 | 2 | 3 |
|---|---|---|---|
| 무게 | 23.43 | 17.42 | 17.6 |
| 무게 + 젖은 흙 (g) | 53.88 | 58.22 | 60.04 |
| 무게 + 마른 흙 (g) | 46.19 | 48.08 | 49.43 |
| 흙의 무게 (g) | 22.76 | 30.66 | 31.83 |
| 물의 무게 (g) | 7.69 | 10.14 | 10.61 |
| 수분 함량(%) | 33.79 | 33.07 | 33.33 |
| 초기 | 종료 | 링의 무게 (g) | 286.38 | - | |
|---|---|---|---|---|---|
| 링 + 흙의 무게 (g) | 395.03 | 389.59 | 젖은 흙의 무게 (g) | 108.65 | 103.21 |
| 판의 무게 (g) | 349.69 | - | 판 + 마른 흙의 무게 (g) | 429.86 | - |
| 마른 흙의 무게 (g) | 80.17 | - | 물의 무게 (g) | 28.48 | 23.04 |
| 수분 함량 (%) | 28.74 | - | - | - | - |
시료의 초기 높이 = 2 cm
시료의 직경 = 6 cm
시료의 비중 = 2.72
● 시료의 면적
A = pi/4*6^2 = 28.27 cm
● 간극비
e = H-Hs/Hs
● 함수비 (Water content, w, %)
w=Ww/Ws, w= 33.79+33.07+33.33/3 = 33.40%
● 초기 흙시료의 높이
2Hs = Ws/A*Gs*rw = 80.17/28.27*2.72*1 = 1.0426cm
● 초기 간극의 높이
Hv=2H-2Hs = 2-1.0426 = 0.9574㎝
● 초기 간극비

● 포화도 (S)
S = wGs / e = 33.40*2.72/0.9185 = 98.91%
●과압밀비 =0.56 0.1 0.2 0.4 0.8 1.6 3.2 6.4 과압밀비 OCR 5.6 2.8 1.4 0.7 0.4 0.2 0.1
| OCR (과응축비) | 5.6 | 2.8 | 1.4 | 0.7 | 0.4 | 0.2 | 0.1 | |
|---|---|---|---|---|---|---|---|---|
| 모래입자크기 (mm) | 0.56 | 0.1 | 0.2 | 0.4 | 0.8 | 1.6 | 3.2 | 6.4 |
● 압축지수
Cc=0.9176472-0.9173019/log3.2-log1.6 = 0.0011
● 선행압밀하중 (Pc)
선행 압밀하중 (Pc)는 e-logp곡선에서 곡률 최대의 점 P를 구하고 이점에서 수평선을 그리고 p점에서 접선을 그린다. 두 직선이 이루는 각을 이등분하는 선을 그린 후 e-logp곡선의 직선 부분의 연장선과 교정의 좌표 Pc로 한다.
따라서 Pc=0.56㎞/㎠
● 압밀침하량의 예측

마무리 글
이번 실험의 가장 중요한 목표는 압밀계수의 측정과 하중이 증가할수록 발생하는 침하가 진행되는 모양과 그에 따른 함수비를 관찰하는 것이 중점적인 사항이었다. 그리고 압밀 곡선을 통하여 흙이 가지고 있는 압축지수, 팽창지수, 선행압밀하중, 시간-침하량 곡선으로 압밀계수, 압축지수를 알아보는 시험이었다.
앞에서 하중이 가해지면 점토의 간극수압이 줄어들고 이에 따라서 유효응력이 증가해서 점토들의 침하가 생긴다고 하였다. 실험 결과에서 보면 하중이 더 가해질 때마다 간극비가 줄어드는 것을 볼 수가 있다. 이는 간극비가 준다는 것은 점토 사이의 간극이 줄어들고 있는 것이며 점토의 부피가 준다는 것을 의미한다.
또한 실험 전에 측정하였던 점토의 함수비와 실험 종료 후의 점토의 함수비를 비교해 보면 실험 후의 함수비가 줄었다는 것을 알 수가 있다. 건조된 시료의 양은 동일하다면 함수비가 줄었다는 것은 점토가 가지고 있던 물의 양이 줄었다는 것으로 해석되는데 이를 통해서 1차 압밀이 일어나는 동안 점토 내에 존재하고 있던 물이 빠져나갔고 간극수압에서 유효응력으로 응력의 전이가 일어났다는 사실을 증명할 수 있다.
오차의 원인은 여러 가지가 있겠지만 제일로 큰 원인 중에 하나는 다이얼게이지를 읽는데 생기는 오차이다. 한 명의 실험자를 통하여 게이지를 읽을 경우에도 오차가 발생하지만 여러 사람이 교대로 돌아가며 측정을 하였기 때문에 개인 오차가 발생하였을 것으로 보인다. 위의 시간-침하량 간의 그래프를 통하여 압밀계수를 알아보았는데 그 그래프에서 점들이 일렬로 이론상의 모습과는 다소 다른 점이 있다면 정확한 시간의 측정과 개인오차에 의한 오차로 보인다.
두 번째로는 시료의 오차이다. 물은 비 압축성이기 때문에 시료의 데이터 값에 그다지 영향을 주지 못한다. 이러한 흙에 우리가 찾지 못하는 공극이 생긴다든지 다른 유기물이 섞인다면 압밀에 의해서 공극이나 유기물은 압축을 일으킬 수가 있으며 이러한 압축은 우리의 데이터 값에 오차를 주는 하나의 요인으로 작용할 수가 있다.
세 번째로는 시험체의 성형에 대한 오차이다. 함수비를 정교하고 시료가 흐트러지지 않도록 주의를 해야 한다는 사실을 알고 있지만, 트리밍 할 때 오차가 생긴 것 같고, 커터링 안의 시료를 압밀링 안으로 불규칙적으로 옮긴 것 같아 오차가 발생한 것으로 본다.
네 번째로는 편심에 대한 오차이다. 실험 초기에 하중이 들어가는 위치에서 여러 각도로 잘 맞아서 들어가는 지를 확인하였다. 이러한 편심 하중이 생긴다면 실험 도중에 중지될 경우도 생기기 때문이다. 이러한 오차의 해결방안으로서는 측정할 때 좀 더 신중하고 공통되는 방법으로 다이얼 게이지를 읽어야 하겠다. 또한 실험기기를 장치를 건드리지 않게 조심하게 측정해야 하겠다.
또 시료를 선택할 때 가급적이면 유기물이 없고 공극이 없는 시료를 선택해야 하겠다. 하중을 줄 때는 편심에 대한 오차를 주지 않게 하기 위해 다각도로 측정하면서 비뚤어지지 않게 잘 맞게 넣어야 하겠다. 또한 그래프를 그리고 나서 압밀계수와 선행압밀응력을 구할 때 개인의 판단에 의한 값을 추정하기 때문에 정확한 값을 알지 못한다는 단점이 있다는 생각이 든다. 이번 실험을 하면서 배운 점은 시간에 따른 하중이 증가함에 따라 압밀이 어느 정도 진행 하다가 12시간이 넘기 시작하면 그 차이가 점점 평형을 이룬다는 점이다.
또한 이때에 다시 하중을 가하면 다시 압밀이 일어나는 현상을 보게 된 것이 참 신기한 점이었다. 이러한 1차 압밀이 끝나고 가만히 놔두면 흙의 배열이나 구조가 바뀌는 2차 압밀로 일어나는 것 또한 하중이 증가함에 따라 log t 법을 보고 알게 되었다. 하지만 초기에는 log t 법이 그다지 정교하지 않고 정확하지 않았지만 점차 log t 법이 점차 자리를 잡아간다는 그래프의 모양을 볼 때 책에서 보았던 log t 법은 루트 t 법보다 좀 더 오랜 시간이 걸린다는 사실을 알 수 있었다.




댓글